Euclid's Definitions, Axioms and Postulates
Euclid's Definitions, Axioms and Postulates: Overview
This Topic covers sub-topics such as Euclidean Geometry, Euclid's Axioms, Fifth Postulate of Euclid, Euclid's Definitions, Second Postulate of Euclid, First Postulate of Euclid, Euclid's Definition of a Point and, Euclidean Dimension
Important Questions on Euclid's Definitions, Axioms and Postulates
Show that, length sum of lengths
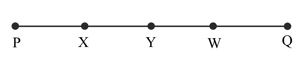
In the given figure, , . With the help of Euclid's axioms find the relation of and ?
A line which lies evenly with the points on itself is called a
A straight line is a line which does not lies evenly with the points on itself.
Which of these following statement is true.
A straight line is a line which lies evenly with the _____ on itself.
State Euclid's definition of a straight line.
The ends of a line segment are points.
A _____ is that which has no part.
In geometry a point, a line and a plane are undefined.
Why do we represent a point as a dot in the definition given by Euclid, even though it has some dimension.
The edges of the surface are
If a straight line falling on two straight lines makes the interior angles on the same side of it taken together less than two right angles, then the two straight lines, if produced indefinitely, meet on that side on which the sum of angles is less than _____ right angles. (two/three/four)
Rewrite Euclid's fifth postulate to understand it in better way.
There exists a pair of straight lines that are everywhere equidistant from one another.
Explain why this statement a direct consequence of Euclid's fifth postulate?
Explain why does Euclid' fifth postulate imply the existence of parallel lines?
Two intersecting lines cannot be perpendicular to the same line.
"A circle can be drawn with any centre and any radius" is Euclids
State Euclids fourth postulate.
"All right angles are equal to one another." is Euclids second postulate.
